Deep Understanding of Roller/Ball Bearing Defect Frequencies

As a condition monitoring technician/analyst, you may have already known the roller/ball bearing frequencies such FTF, BSF, BPFO and BPFI, and some of you may even remember the formulae or have an Excel spread sheet to calculate these frequencies. You may have also noted that the theoretical defect frequencies may not exactly match the defect frequencies in real vibration spectra.  Why? Are these formulae are always correct? Under what conditions will these formulae give reasonable results? To answer these questions, we need to know how these defect frequencies are derived.

 

Let’s look at a roller or ball bearing with its outer raceway fixed and the inner raceway free to rotate. The pitch diameter is denoted with D, and roller diameter with d. The contact angle in this example is zero. The inner race is rotating at an angular speed of ω. The number of balls/rollers is n.

 

Assumption1 : All rolling elements are rolling without any slips between the roller/ball and raceways.

 

This assumption implies:

(1): No clearances between each ball/roller and either the inner or outer raceway.

(2): The friction on the contact points between a ball and any a raceway should be big enough to prevent any slipping.

 

Assumption 2:  The rotational axis of each ball/roller keeps the same angle with the shaft, i.e. parallels with the shaft if the contact angle is zero, or keeps the same angle with the shaft that equals to the contact angle.

 

This assumption holds with cylindrical rollers, but may not be true for balls, particularly when the ball is at the non-loading zone.

 

3. Cage rate or Fundamental Frequency

 

To find the cage rotating speed, we only need to know the speed of a point on the cage. We can select a special point C as this point. We say this point is special because both cage and the ball/roller have the same speed. To find out the speed at Point C, let’s look at the ball/roller in the light green colour. Due to our assumptions, point B on this ball/roller is stationary, and point A should have the same speed as the contact point on the inner raceway, i.e.

                                                          .

 

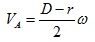The roller is actually doing the so called planar movement, which can be treated as rigid body rotating about an instant axis at point B. Therefore, the speed at point C can be easily obtained as

                                                     

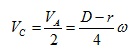
Now we’ve got the speed at point C on the cage, the angular speed of the cage can be derived as

4. Ball Pass Frequency Outer race (BPFO)

 

Imagine that there is a defect on the outer raceway, when the cage has one revolution, all n balls/rollers will pass the defect once. This means that the ball pass the outer race defect frequency is n times the cage rate, which gives

This is the frequency that all balls pass one defect on the outer raceway, so it is also the outer race defect frequency.

 

5. Ball Spin Frequency (BSF)

To find out the ball spin speed, let us check a single ball marked as light green in the figure shown on the right hand side.  When a ball spins for one revolution, the ball moves from poison P1 to P2, and the path on the outer raceway this ball travelled is marked as read colour. From position P1 to position P2, the cage swept an angle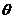

Now we know the angle the ball rotated, that is, (a full revolution). To find the angular speed of the ball, we need to find out the time it spent. To this end, we check the cage. It rotated an angle 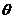at a angular speed of 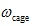. The time used to rotate such an angle is

The angular speed of the ball can be obtained as

Is the ball/roller spin frequency is the ball defect frequency? The answer is no. Why? In one revolution of the ball, the defect hits the raceways TWICE, one on the outer raceway (the impacting sensed by the accelerometer is stronger), and the other on the inner raceway (this impacting sensed by the accelerometer is weaker). Therefore, the ball defect frequency should be TWO TIMES the ball spin frequency. The ball pass frequency is

6. Ball Pass Frequency Inner race (BPFI)

 

Now we’ve got two components that rotate around the centre point O of the bearing, one is the inner race, which has an angular speed of ω,  and another one is the cage with a speed of 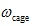. Both components rotate at the same direction but with different speeds. There are several ways to calculate the BPFI. Here, we actually don’t need to derive the BPFI in a lengthy way, but “discover” it by changing your observing point.

To better understand the speed that the balls pass a point on the inner raceway, imagine that you close your eyes and jumped onto the cage and rotate together with the cage. Now, open your eyes, what you can see when standing on the cage? The cage stands still, all balls rotate around a fixed point on the cage, and the outer race way is now rotating (at the cage rotational speed)! Of course, the inner race is still rotating, but at a lower angular speed, which is the speed of the inner race relative to the cage

The above formula is actually the frequency the inner raceway pass one ball. Multiplying by the number of roller elements, we get the BPFI, i. e.

 

                                            

 

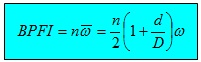
BPFI is also the inner race defect frequency.